Pi: Unlocking the never-ending constant

14 Mar '25

Have you ever wondered about the constant pi (π) ? In schools, we were taught that it is a constant which is used to calculate the circumference and area of a circle. The pi (π) constant represents the ratio of a circle's circumference to its diameter (represented by d or 2r), i.e. π = C/2r. Its significance is that no matter the size of the circle, the ratio of its circumference to its diameter will always be equal to this constant value called pi (π).

In Singapore's primary schools and lower secondary math classes, pi is approximated using a rational number, 22/7. At upper secondary, when students are better able to handle abstract concepts like representing a constant value with a symbol, they key in the π symbol into their scientific calculators to handle calculations involving pi. An interesting bit about pi is that since it is an irrational number, the constant number extends indefinitely. There are various forms of longest pi competitions such as calculating or reciting as many digits of pi as possible. In June 2024, TechRadar reported that a team had successfully calculated pi to 202 trillion digits (TechRadar, 2024), nearly doubling the previous record. Of course, this can be done only with the help of supercomputers and improved algorithms.

The next question which probably comes into our mind is how can we determine the exact value of pi? To be exact, its value cannot be fully calculated because it extends indefinitely. However, it can be approximated with ever increasing precision using various mathematical methods. These methods can be broken down into 3 methods; geometric (measure), Monte-Carlo (probability) and the Infinite Series. As a matter of personal interest, I decided to explore the Infinite Series in greater detail in this article, leaving the curious reader to find out more on the other two approaches.

Infinite Series

The Infinite series is the sum of infinitely many numbers related in a given wayand listed in a given order. Infinite series are useful in mathematics and in such disciplines as physics, chemistry, biology, and engineering (Britannica, 2025) Given that S is the sum of the series and n is the number of terms, the sum of the series approaches a fixed number as n becomes larger and larger, the series is said to converge. An infinite series that does not converge is said to diverge. In the case of divergence, no value of a sum is assigned (Britannica, 2025).

There are many types of infinite series. They differ mainly in their convergence properties and the rules governing the terms. To approximate the value of pi, the infinite series of Leibniz (Leibniz series) and Ramanujan (Ramanujan's series) come to mind. The Chudnovsky algorithm which is used in breaking the world record in the calculating the most digits is based on Ramanujan's series. For something more palatable, let us look into the Leibniz series.

Leibniz series

The Leibniz series is an infinite series that provides an approximation of π. It is given by the formula:

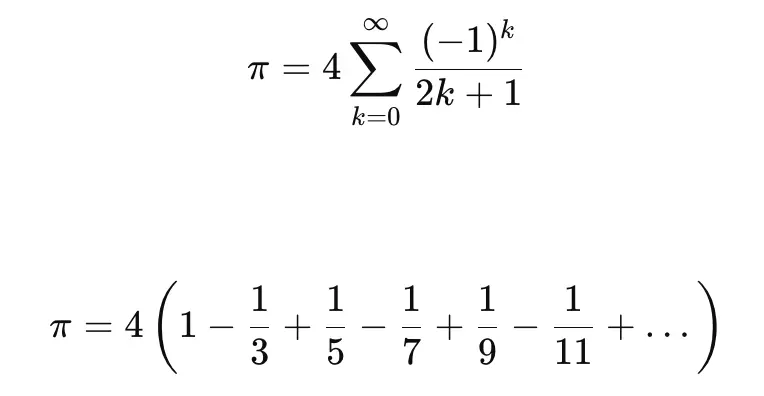
The series can derived from the Taylor series, which is the power series for the inverse tangent function. For simplicity, we will not look into deriving the power series for the inverse tangent function. So, as a starting point, we shall treat it as proven 😊.

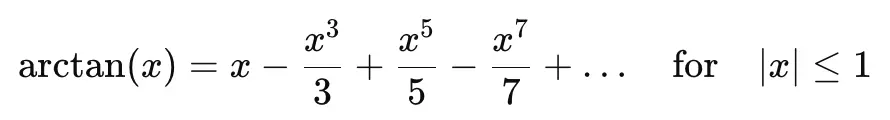
By substituting x = 1, we get:

We also know that the inverse tangent of 1 is π / 4. We can easily derive this result with a right-angle isosceles triangle.

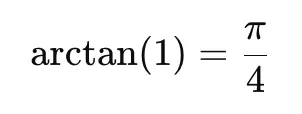
So we have:

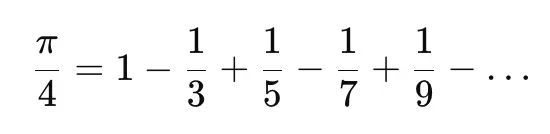
Multiplying the equation by 4, we obtain

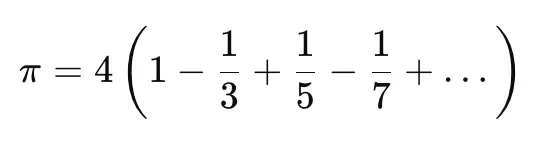
which is the Leibniz series.

Note that the Leibniz series converges slowly, meaning that each additional term only improves the value of pi slightly. For example, calculating pi to 10 correct decimal places using direct summation of the series requires precisely five billion terms (Wikipedia, 2025). Nonetheless, it is easy to understand, thus serving as a good starting point to approximate pi.

The calculator below computes the value of pi using the Leibniz Series. You can enter the desired number of terms to increase the accuracy of the approximation.

We have explored the ubiquitous pi (π) in this article. From its definition as the ratio of a circle's circumference to its diameter, we have examined the use of Leibniz series to approximate the value of pi. I hope that this has been enriching and serves as fodder for further exploration of pi. Happy Pi Day!